
Ссылки
2. Пропорциональность
Человеческий глаз привык к определенному соотношению длины и ширины предметов (рис. 64). На приведенном рисунке рамки 3, 13 и 14 по размерам, т. е. пропорциям, лучше, чем все остальные. Колонна и столб, например, шириной свыше 1 м и небольшой высоты, окрашенные в один тон, будут казаться тяжелыми; если же колонну разбить на ряд вертикальных полос и окрасить их разными колерами, то она будет производить впечатление изящной.
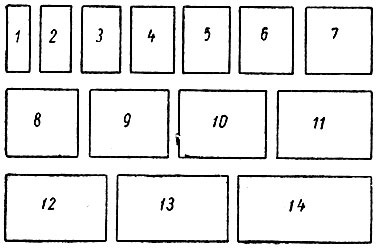
Рис. 64. Рамы с различным соотношением длины и ширины
В архитектуре размеры главных частей (например, колонн, архитравов, карнизов и пр.) соблюдаются для каждого стиля; однако из-за наличия множества архитектурных обломов, определение их пропорций предоставляется вкусу архитектора, строителя. Кроме того, строительное искусство постоянно требует новых и новых архитектурных комбинаций, вызывающих необходимость изменения пропорций.
Пропорции можно наблюдать в разрезных листьях растений, например, в листке клена (см. рис. 60). Рисованный акантовый лист отличается еще большей сложностью: он состоит из сильно расчлененных частей, в величине которых соблюдена пропорциональность (рис. 65).

Рис. 65. Рисованный лист Аканта
Соблюсти единство пропорций легче всего в том случае, если имеются в своем распоряжении три элемента формы, из которых один больше других, а остальные два по величине равны между собой. Например, вывески, состоящие из двух или трех строчек, надо писать таким образом, чтобы одна строка состояла из более крупных букв и была длиннее других; тогда эти строки будут ей подчинены и в целом мы получим впечатление гармоничного построения.
Рассмотрим с этой точки зрения лист клена (см. рис. 60). Центральная его часть самая длинная, боковые части короче, следующие за ними еще короче, а последние, находящиеся по двум сторонам стебля, самые короткие. В силу привычки к пропорциональному построению листьев мы сразу заметим изменение пропорций. Попробуем укоротить среднюю часть листа, сделаем ее одинаковой с боковыми частями (рис. 66), и сразу станет заметно, что гармония листа нарушена. Теперь попробуем удлинить среднюю часть листа (рис. 67). Гармоничная форма листа также нарушена.
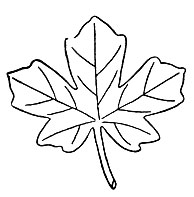
Рис. 66. Укороченный лист клена
Подобный опыт можно проделать с листом каштана и со всяким другим сложным листом.
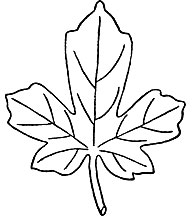
Рис. 67. Удлиненный лист клена
Особый род пропорциональности - правильность. Среди геометрических форм этого рода можно назвать треугольники, прямоугольники, правильные многоугольники. В числе тел, ограниченных прямыми линиями, мы находим куб, а среди тел, ограниченных кривыми линиями и поверхностями, - круг, эллипс, овал, шар, разные цилиндры и конусы с правильным основанием. Правильный пятиугольник можно быстро построить (рис.68), пользуясь деревянным прямоугольным треугольником Рево (длинный катет 200 мм, короткий - 65 мм с углами 72 и 18°).
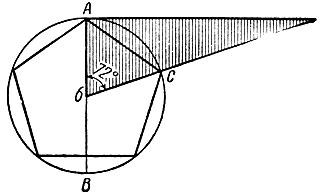
Рис. 68. Пользование прямоугольным треугольником Рево для построения правильного пятиугольника
Мастера росписи и художники-декораторы должны всегда обращать большее внимание на пропорциональность; но они часто грешат против нее, делая панно слишком низкими или помещая на небольших площадях крупные изображения.
Надо помнить, что два одинаковых протяжения никогда не должны следовать одно за другим в вертикальном направлении. Протяжения всегда должны иметь различную величину не только для лучшей пропорциональности, но и для большего разнообразия.
В орнаментации следует постоянно помнить о пропорциональности. Орнаментированное стенное панно пропорционально всей поверхности стены; пропорциональность должна существовать и между отдельными ее частями. В полосном орнаменте расстояние между полосами тем значительнее, чем они шире, и наоборот.
Существуют законы пропорционального деления на неравные отрезки. Правило "золотого сечения", например, дает максимальное число отношений при делении на две части.
Простым гармоничным сочетанием являются два отрезка: 0,382 и 0,618, в сумме равные 1,00. Следовательно, при расчерчивании стены высоту фриза принимают кратной 0,382, а высоту неорнаментированной плоскости стены - кратной 0,618.
Приведем ряд примеров гармоничного деления по принципу "золотого сечения" на 2, 3, 4 и 5 отрезков.
| 2 отрезка | 3 отрезка | 4 отрезка | 5 отрезков |
|---|---|---|---|
| 0,382 | 0,191 | 0,106 | 0,061 |
| 0,618 | 0,309 | 0,171 | 0,099 |
| 0,500 | 0,276 | 0,160 | |
| 0,447 | 0,260 | ||
| 0,420 | |||
| 1,000 | 1,000 | 1,000 | 1,000 |
В архитектуре стены, разделенные по правилам пропорционального деления на два отрезка, называют триадой, на три отрезка - тетрадой, на четыре отрезка - пектадой, на пять отрезков - гексодой.
стеклянные шторы для душевой кабины
|
ПОИСК:
|
При копировании обязательна установка активной ссылки:
http://remont.townevolution.ru/ 'Ремонт помещений и отделка зданий'